4. Mastermind¶

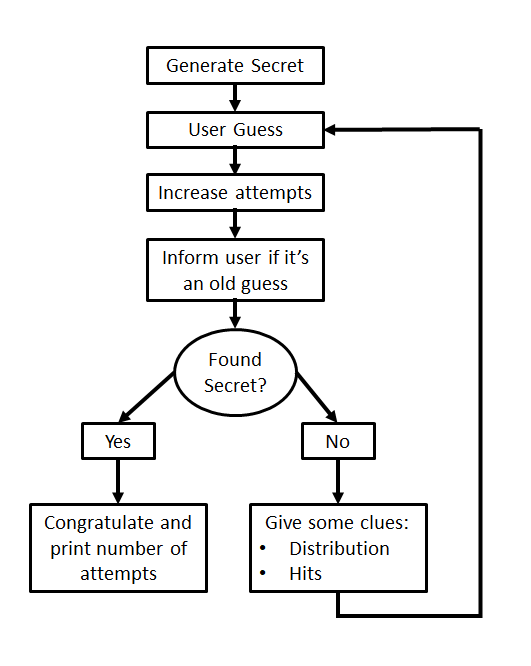
En esta ocasión vamos a implementar una versión para un jugador del juego de mesa Mastermind. Originalmente, el Mastermind es un juego de ingenio para dos jugadores en el que cada uno tiene que adivinar la secuencia secreta de colores que ha construido su oponente. Para ello, cada jugador hace una propuesta y el oponente le devuelve una serie de pistas que le ayudarán a refinar su propuesta en el siguiente turno. La versión que os proponemos nosotros tiene unas reglas simplificadas:

El código genera una secuencia secreta aleatoria de dos colores (Rojo y Verde)
El jugador tiene que averiguarla
El jugador no puede repetir secuencias, en caso de hacerlo, tiene que recibir un aviso
El código debe de dar pistas al usuario sobre si la distribución de colores (número de rojos y número de verdes) coincide con el de la secuencia secreta y sobre el número de colores que ha acertado
Cuando el usuario acierte la secuencia secreta, el código debe imprimir el número de intentos

A continuación proporcionamos un diagrama de flujo que resumen las reglas anteriores:

El resultado debe ser algo así:

4.1. Generación de la secuencia secreta¶

Para inicializar el juego vamos a implementar una función gen_secret(size) que se encargue de generar una secuencia aleatoria y secreta de rojos R y verdes G. La función recibe un único argumento size con la longitud de la secuencia que será proporcional a la dificultad del juego. La salida de gen_secret también será única, devolviendo una variable tipo STRING con la secuencia de G’s y R’s (e.g. “RRGG”).

Solución:¶

import random

def gen_secret(size):
    options=["R","G"]
    pattern=[]
    for i in range(size):
        pattern.append(options[random.randint(0,1)])
    secret="".join(pattern)
    return secret

gen_secret(size=4)

'RGRR'

Note

En programación existen muchas maneras de implementar la misma función, y eso no implica que unas estén bien y otras no. La intuición más sencilla nos suele sugerir utilizar un bucle y una función que eija uno entre dos valores que serán usados como índices a la hora de indexar el caracter R o el caracter G. Otra alternativa podría ser la siguiente:

def gen_secret(size):
    options=list("RRRRRRRRRRGGGGGGGGGG")
    random.shuffle(options)
    secret="".join(options[:size])
    return secret

En este caso hacemos uso de la función random.shuffle para aleatorizar los elementos de una lista, para quedarnos con los size primeros elementos de la lista resultante.

4.2. Elección de la secuencia candidata¶

Para que el jugador introduzca su secuencia propuesta, vamos a implementar una función input_seq(size) para que el usuario introduzca una secuencia STRING de Rojos y Verdes (e.g. “RRGG”). El código debe seguir preguntando al usuario en caso de que no introduzca el número de colores requerido o en caso de que utilize letras diferentes de “R” o “G”.

Esta función recibe la longitud de la secuencia en la variable size y debe devolver la secuencia de colores en formato STRING.

Solución:¶

def input_seq(size):
    guess=input("\nInput a sequence of R's and G's with length {}: ".format(size)) 
    
    while (guess.count("R")+guess.count("G")!=size) or (len(guess)!=size):
        print("The sequence can only contains G's and R's and must have length {}".format(size))
        guess=input("Guess a sequence of R's and G's with length {}: ".format(size))
    
    return guess

input_seq(4)

Input a sequence of R's and G's with length 4: RRGGG
The sequence can only contains G's and R's and must have length 4
Guess a sequence of R's and G's with length 4: RRGX
The sequence can only contains G's and R's and must have length 4
Guess a sequence of R's and G's with length 4: RRGG

'RRGG'

Note

La dificultad de esta función reside en verificar que la secuencia proporcionada por el jugador sólo contiene R’s y G’s y que su longitud no excede el valor definido por la variable size. En nuestra solución hemos usado la condición buleana:

(guess.count("R")+guess.count("G")!=size) or (len(guess)!=size)

Esta expresión hace uso de la función count de las variables de tipo STRING, para verificar que las letras de la secuencia sólo se corresponden con las permitidas.

4.3. Plot de la secuencia¶

El método plot_seq(guess) que vamos a codificar recibe una secuencia de colores en la variable guess de tipo STRING (e.g. “RRGG”) e imprime esa misma secuencia con puntos de colores. Esta función no devuelve ningún valor.

Tip

Para imprimir texto en color necesitamos usar la librería termcolor. Prueba este código en una celda:

from termcolor import colored
print(colored("●","red"))

Si el import no reconoce la librería ejecuta este comando en otra celda para instalarla (sólo tienes que ejecutarlo una vez):

! pip install --user termcolor

Solución:¶

from termcolor import colored

def plot_seq(guess):
    for color in guess:
        if color=="R":
            print(colored("●","red"),end="")
        elif color=="G":
            print(colored("●","green"),end="")
        else:
            print("●",end="")
    print()

plot_seq("RRGG")

●●●●

4.4. Chequeo de la distribución de colores¶

Una de las pistas que debe devolver nuestro juego es si el número de rojos R y el número de verdes G de la secuencia proporcionada por el jugador coincide con la secuencia secreta. Para eso vamos a construir la función check_distribution(guess,secret). Esta función recibe dos argumentos:

guess es una variable tipo STRING que contiene la secuencia de colores proporcionada por el jugador
secret es una variable tipo STRING que contiene la secuencia secreta

La función debe chequear si el número de R’s y de G’s coincide entre ambas secuencias. La función debe devolver una variable BOOL indicando si el número de colores es el mismo en ambas secuencias.

Solución:¶

def check_distribution(guess,secret):
    if guess.count("R")==secret.count("R") and guess.count("G")==secret.count("G"):
        return True
    else:
        return False

A modo de ejemplo, vamos a invocar a esta función con dos secuencias diferentes, la primera de ellas contiene la misma disribución de colores que la secuencia secreta. Si la función check_distribution está bien implementada debe devolver el valor True. La segunda contiene una distribución de colores diferentes, por lo que la función check_distribution debe devolver el valor False.

check_distribution(guess="GRGR",secret="GGRR")

True

check_distribution(guess="GRRR",secret="GGRR")

False

4.5. Chequeo del número de aciertos¶

La segunda de las pistas que el juego tiene que proporcionar es el número de aciertos. Para ello vamos a implementar la función check_coincidences(guess,secret). Este método recibe los mismos argumentos que la función check_distribution, es decir, la secuencia de colores del usuario guess y la secuencia de colores secreta secret. La función check_coincidences debe analizar las posiciones de los colores de la secuencia del usuario y de la secuencia secreta y devolver el número de aciertos.

Solución:¶

def check_coincidences(guess,secret):
    out=[]
    for i in range(len(guess)):
        if guess[i]==secret[i]:
            out.append(1)
        else:
            out.append(0)
    number_of_coincidences=sum(out)
    return number_of_coincidences

De nuevo, vamos a validar el funcionamiento de la función probando diferentes secuencias con diferentes coincidencias entre la secuencia proporcionada por el jugador guess y la secuencia secreta secret.

check_coincidences(guess="RRGG",secret="GGRR")

check_coincidences(guess="GRGR",secret="GGRR")

check_coincidences(guess="GRRR",secret="GGRR")

check_coincidences(guess="GGRR",secret="GGRR")

4.6. Fin de juego¶

Por último, vamos a implementar la función match(guess,secret). De nuevo, esta función recibe los mismos dos argumentos:

guess es una variable tipo STRING que contiene la secuencia de colores proporcionada por el jugador
secret es una variable tipo STRING que contiene la secuencia secreta

La función debe devolver True en caso de que las secuencias coincidan y False en caso contrario. Esta función es trivial, y su objetivo es, simplemente, hacer el código del juego más legible.

Solución:¶

def match(guess,secret):
    if guess==secret:
        return True
    else:
        return False

match(guess="RRGG",secret="RRGG")

True

match(guess="RRGR",secret="RRGG")

False

4.7. Juego completo¶

El último paso es utilizar todas las funciones implementadas hasta el momento para construir nuestra versión simplificada del Mastermind. Vamos a añadir un sistema de conteo del número de intentos. De esta forma, si decides jugar con más personas, podrás decidir quién es el vencedor como aquel jugador que haya realizado las mejores hipótesis.

Solución:¶

from termcolor import colored
import random

size=4
guesses=[]
attempts=0

# Generates a secret
print("Generate secret with length: {}".format(size))
print("......")
secret=gen_secret(size)

while True:
    # Ask the user for a guess
    guess=input_seq(size)
    attempts=attempts+1
    
    # Plot the sequence of colored points
    plot_seq(guess)
    
    # Inform the user if that guess was already used
    if guess in guesses:
        print(" - Combination already used")
    else:
        guesses.append(guess)      

    # Check if we found the solution
    if match(guess, secret)==True:
        print("Congrats!!")
        break
    else:
        # Check if we found the right R's and G's distribution
        if check_distribution(guess, secret)==True:
            print("Distribution: OK. ")
        else: 
            print("Distribution: WRONG. ")
        
        # Check the number of coincidences
        print("Hits: {}".format(check_coincidences(guess, secret)))

print("You needed {} attempts".format(attempts))

Generate secret with length: 4
......

Input a sequence of R's and G's with length 4: RRGG
●●●●
Distribution: WRONG. 
Hits: 1

Input a sequence of R's and G's with length 4: GGGR
●●●●
Distribution: OK. 
Hits: 2

Input a sequence of R's and G's with length 4: RGGG
●●●●
Distribution: OK. 
Hits: 2

Input a sequence of R's and G's with length 4: GRGG
●●●●
Distribution: OK. 
Hits: 2

Input a sequence of R's and G's with length 4: GGRG
●●●●
Congrats!!
You needed 5 attempts

4.8. Extensiones del Juego¶

El Mastermind es un juego muy sencillo pero con muchas posibilidades de complicarse. Utilizar secuencias más largas es una de ellas, pero podemos incrementar el número de colores o incluso utilizar símbolos diferentes. Aquí os proponemos algunas alternativas para que siguáis mejorando vuestras habilidades de programación:

Implementar una versión con más colores
Construir un Mastermind en el que además de los colores, entren en juego el típo de símbolos, por ejemplo, puntos “●” y cuadrados “■”
Añadir un temporizador para poder echar partidas contrarreloj
Mejorar el interfaz para que se parezca al interfaz clásico del Mastermind juego de mesa

Playing Python

Mastermind

Contents

4. Mastermind¶

4.1. Generación de la secuencia secreta¶

Solución:¶

4.2. Elección de la secuencia candidata¶

Solución:¶

4.3. Plot de la secuencia¶

Solución:¶

4.4. Chequeo de la distribución de colores¶

Solución:¶

4.5. Chequeo del número de aciertos¶

Solución:¶

4.6. Fin de juego¶

Solución:¶

4.7. Juego completo¶

Solución:¶

4.8. Extensiones del Juego¶