Arkanoid
Contents
2. Arkanoid¶

En este capítulo vamos a programar un juego clásico que muchos conocimos como Arkanoid. En realidad, este juego es una exploitation de otro juego clásico llamado Breakout. Si buscas imágenes por internet verás que las similitudes son asombrosas.
Si te interesa el mundo de los videojuegos, te recomendamos leer la historia del Breakout, diseñado para la mítima compañía Atari por Steve Wozniak, fundador de Apple junto a Steve Jobs. El resumen de esa historia apasionante es que uno de los fundadores de Atari, Nolan Bushnell, encargó a Steve Jobs el desarrollo de un prototipo del Breakout que debía tener listo en cuatro días a cambio de 750$ (de 1975) y un bonus por cada microchip que consiguiera ahorrarse. La tendencia de Atari era la de crear videojuegos con entre 150 y 170 chips que los hacían caros y complicados de construir. Steve Jobs contactó con su amigo Steve Wozniak, empleado de Hewlett-Packard, al que ofeció la mitad de los beneficios que consiguieran. Wozniak consiguió construir en cuatro noches un prototipo funcional con solo 42 chips. Bushnell quedó tan satisfecho que le pagó a Steve Jobs 5000$ por el trabajo, quien a su vez sólo pagó a Steve Wozniak 350$.
La dinámica de juego del Arkanoid es muy sencilla. En la parte inferior de la pantalla hay una plataforma que el usuario puede mover de derecha a izquierda y que funciona a modo de raqueta. Con esta plataforma, el usuario devuelve contínuamente una pelota que puede rebotar en cualquiera de las paredes y en una colección de ladrillos que desaparecen con cada impacto. El objetivo es eliminar todos los ladrillos que se encuentran en la parte superior de la pantalla.
Aqui puedes ver una pequeña demostración del juego:
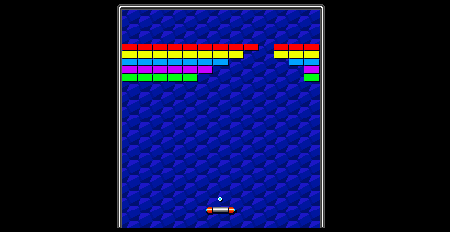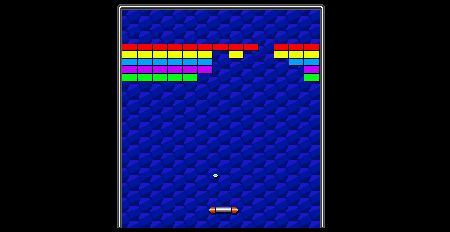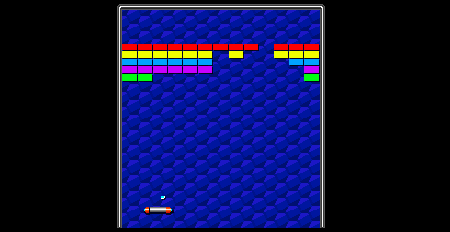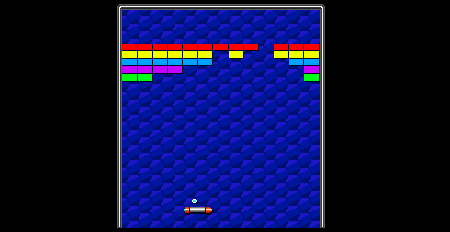
See also
Puedes leer más sobre el Blockout aquí y sobre el Arkanoid aquí.
Y si te interesa la historia de Atari, hay múltiples libros que la explican detalladamente. O bien puedes escucharte la primera parte de este podcast en el que la repasan con mucho detalle.
2.1. Desarrollo del interfaz gráfico¶
Para el entorno gráfico, vamos a usar la librería turtle. Esta librería emula el comportamiento del lenguaje de dibujo del que ya hemos hablado en el capítulo LOGO.
Para pintar los elementos del juego, vamos a utilizar las funcciones draw_circle(x, y, radius) y draw_rectangle(x, y, width, height). Como indican sus nombres, estas funciones dibujan circulos y rectangulos en las coordenadas (x, y) con unas dimensiones determinadas.
Las coordenadas en la librería turtle se refieren al centro de la pantalla y crecen positivamente en el eje X hacia la derecha y en el eje Y hacia arriba siguiendo el siguiente esquema:
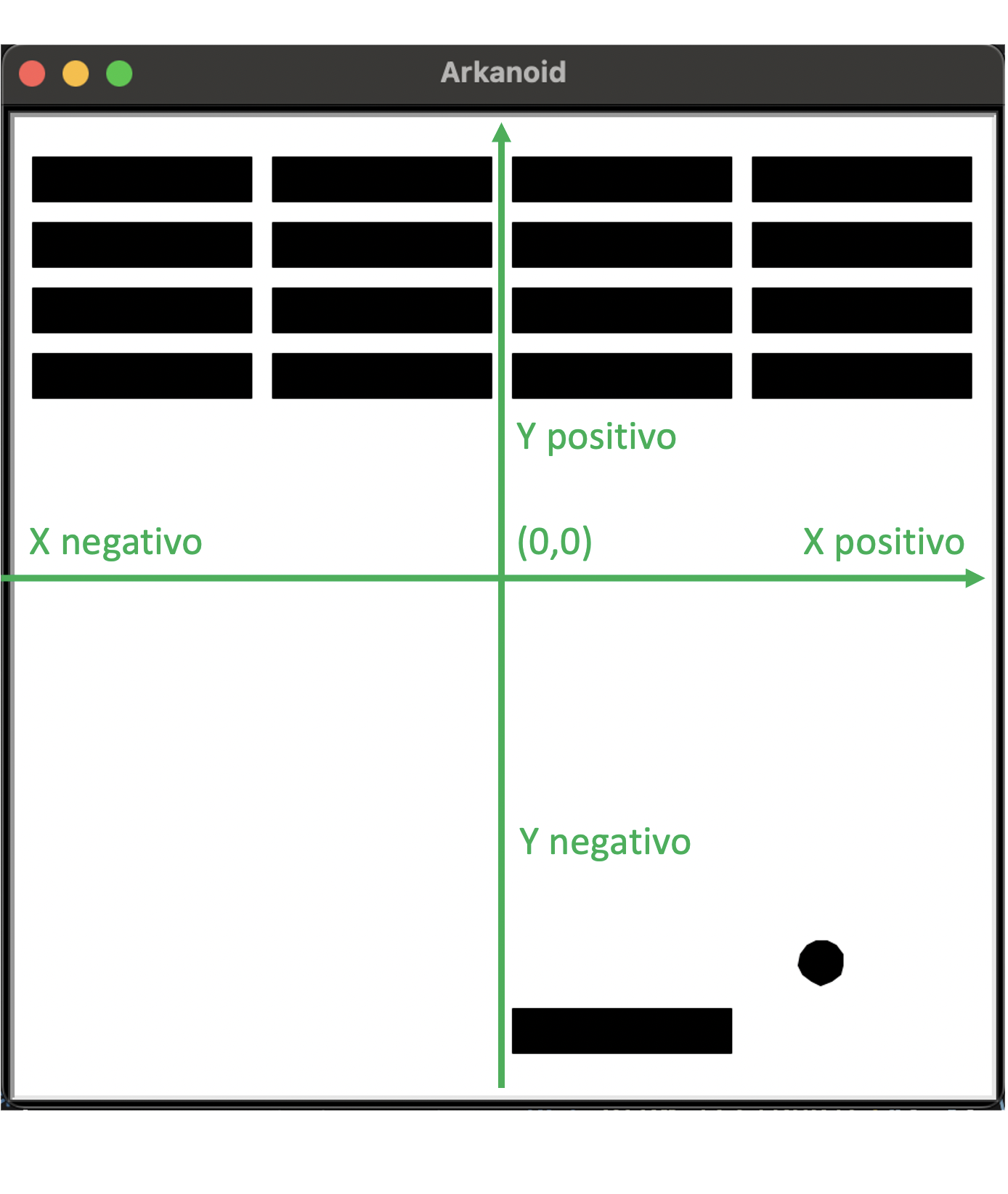
See also
Si quieres consultar los comandos de la librería turtle puedes visitar su página web aquí.
import turtle as t
def draw_circle(x, y, radius):
t.up()
t.setpos(x, y)
t.down()
t.begin_fill()
t.circle(radius)
t.end_fill()
t.up()
t.setpos(-x-radius, -y-radius)
t.down()
def draw_rectangle(x, y, width, height):
t.up()
t.setpos(x, y)
t.down()
t.begin_fill()
for count in range(2):
t.forward(width)
t.left(90)
t.forward(height)
t.left(90)
t.end_fill()
t.up()
t.setpos(-x-width, -y-height)
t.down()
2.2. Parámetros del juego¶
Para controlar los parámetros del juego, vamos a crear el diccionario game_params en el que vamos a definir las dimensiones y las velocidades de movimiento de los diferentes componentes de nuestra pantalla.
import math
game_params = {
# CONSTANTS
"ball_radius": 10,
"ball_speed": 10,
"pad_speed": 10,
"pad_width": 100,
"pad_height": 20,
"screen_width": 460,
"screen_height": 460,
"target_width": 100,
"target_height": 20,
"target_count_per_row": 4,
"target_count_per_column": 4,
"padding":10,
# VARIABLES
"ball_position_x": 0,
"ball_position_y": 0,
"ball_sloping_positive": True,
"ball_angle": 50,
"pad_position_x": 0,
"pad_position_y": -200,
"end_game": False,
"targets_on_map": []
}
Note
En la sección de constantes se definen el tamaño y velocidad de la pelota (ball), el tamaño y velocidad de la plataforma que hace de raqueta (pad) y el tamaño, número de filas y columnas del muro de ladrillos (target). Como ves, nuestro juego contiene 4 filas y 4 columnas con ladrillos de tamaño 100x20.
En la sección de variables se almacenarán los datos que irán variando en función del progreso del juego. Los más importantes son la posición de la raqueta y la posición de la pelota así como el angulo y la pendiente de su movimiento.
2.3. Calculo de las coordenadas de los ladrillos¶
Para que nuestro juego sea muy flexible y podamos definir diferentes niveles de dificultad basados en diferentes distribuciones de ladrillos, vamos a programar la función calc_targets_positions(game_params) que recibe como único argumento de entrada el diccionario con los parámetros del juego y devuelve una lista de tuplas (x, y) que representan las coordenadas en las que empieza cada ladrillo.
Tip
Recuerda lo que hemos explicado antes respecto a la referencia de las coordenadas para la librería turtle.
Solución:¶
def calc_targets_positions(game_params):
targets_positions = []
x_init = -game_params["screen_width"]/2 + game_params["padding"]
y_init = game_params["screen_height"]/2 - 4 * game_params["padding"]
x,y = x_init, y_init
for i in range(game_params['target_count_per_column']):
for j in range(game_params['target_count_per_row']):
targets_positions.append((x, y))
x += game_params['target_width'] + game_params['padding']
y -= game_params['target_height'] + game_params['padding']
x = x_init
return targets_positions
Si invocamos a esta función con los parámetros anteriores game_params, debemos obtener 16 coordenadas correspondientes a los 16 ladrillos (4 filas por 4 columnas) que debemos romper.
calc_targets_positions(game_params)
[(-220.0, 190.0),
(-110.0, 190.0),
(0.0, 190.0),
(110.0, 190.0),
(-220.0, 160.0),
(-110.0, 160.0),
(0.0, 160.0),
(110.0, 160.0),
(-220.0, 130.0),
(-110.0, 130.0),
(0.0, 130.0),
(110.0, 130.0),
(-220.0, 100.0),
(-110.0, 100.0),
(0.0, 100.0),
(110.0, 100.0)]
2.4. Inicializar objetivos¶
La salida de la función anterior nos devuelve las coordenadas de los objetivos. Estos valores tenemos que inicializarlos en la clave “targets_on_map” del diccionario game_params. Vamos a introducir esta inicialización dentro de una función init_targets() que ni recibe ni devuelve ningún valor.
Tip
Como ya hemos comentado en un capítulo anterior, el uso de variables globales no se suele recomendar a los programadores noveles ya que abre la puerta a muchos errores difíciles de detectar. En este caso vamos a utilizar la variable game_params como variable global ya que todos los métodos de nuestro programa van a necesitar tener acceso a ella. Si la utilizamos como variable global, no necesitamos pasarla por argumento.
Aún así, si no te sientes muy cómodo con el uso de variables globales, puedes incluirla como argumento de todas las funciones que hagan uso de ella.
Solución:¶
def init_targets():
game_params["targets_on_map"] = calc_targets_positions(game_params)
Si invocamos a esta función y verificamos la clave “targets_on_map”, deberíamos obtener la lista de coordenadas de los ladrillos:
init_targets()
print(game_params["targets_on_map"])
[(-220.0, 190.0), (-110.0, 190.0), (0.0, 190.0), (110.0, 190.0), (-220.0, 160.0), (-110.0, 160.0), (0.0, 160.0), (110.0, 160.0), (-220.0, 130.0), (-110.0, 130.0), (0.0, 130.0), (110.0, 130.0), (-220.0, 100.0), (-110.0, 100.0), (0.0, 100.0), (110.0, 100.0)]
2.5. Calcular ángulo de rebote de la pelota¶
Cada vez que la raqueta (pad) golpée la pelota, o cada vez que la pelota golpée un ladrillo o una pared, hay que calcular el ángulo de rebote. En este apartado vamos a implementar la función calc_ball_rebound_angle() que realiza esos cálculos.
La lógica del rebote es la siguiente:
si la clave “ball_sloping_positive” del diccionario game_params es True, significa que la pelota se dirige hacia los ladrillos, por lo que el angulo de rebote será igual a 175 - game_params[“ball_angle”]
si la clave “ball_sloping_positive” del diccionario game_params es False, significa que la pelota se dirige hacia la raqueta, por lo que el angulo de rebote será igual a 175 + game_params[“ball_angle”]
Note
El utilizar un valor de 175º en lugar de 180º tiene como propósito añadir cierta contraintuitividad en al rebote de la pelota, lo que incrementa la dificultad del juego.
Solución:¶
def calc_ball_rebound_angle():
param = 175
if game_params["ball_sloping_positive"]:
angle = param - game_params["ball_angle"]
else:
angle = param + game_params["ball_angle"]
return angle
2.6. Detección de impactos con la raqueta¶
Para que nuestro programa detecte si la pelota ha golpeado la raqueta, vamos a codificar la función has_impact(x_ball, y_ball, x_pad, y_pad, pad_width, pad_height) que recibe como argumentos:
x_ball: la coordenada x de la pelota
y_ball: la coordenada y de la pelota
x_pad: la coordenada x de la raqueta
y_pad: la coordenada y de la raqueta
pad_width: el ancho de la raqueta
pad_height: el alto de la raqueta
Y devuelve un booleano que indica si la bala ha impactado en el pad.
Para detectar si la bala ha impactado en el pad, verificamos si la pelota está tocando o dentro del pad como se puede ver en este esquema:
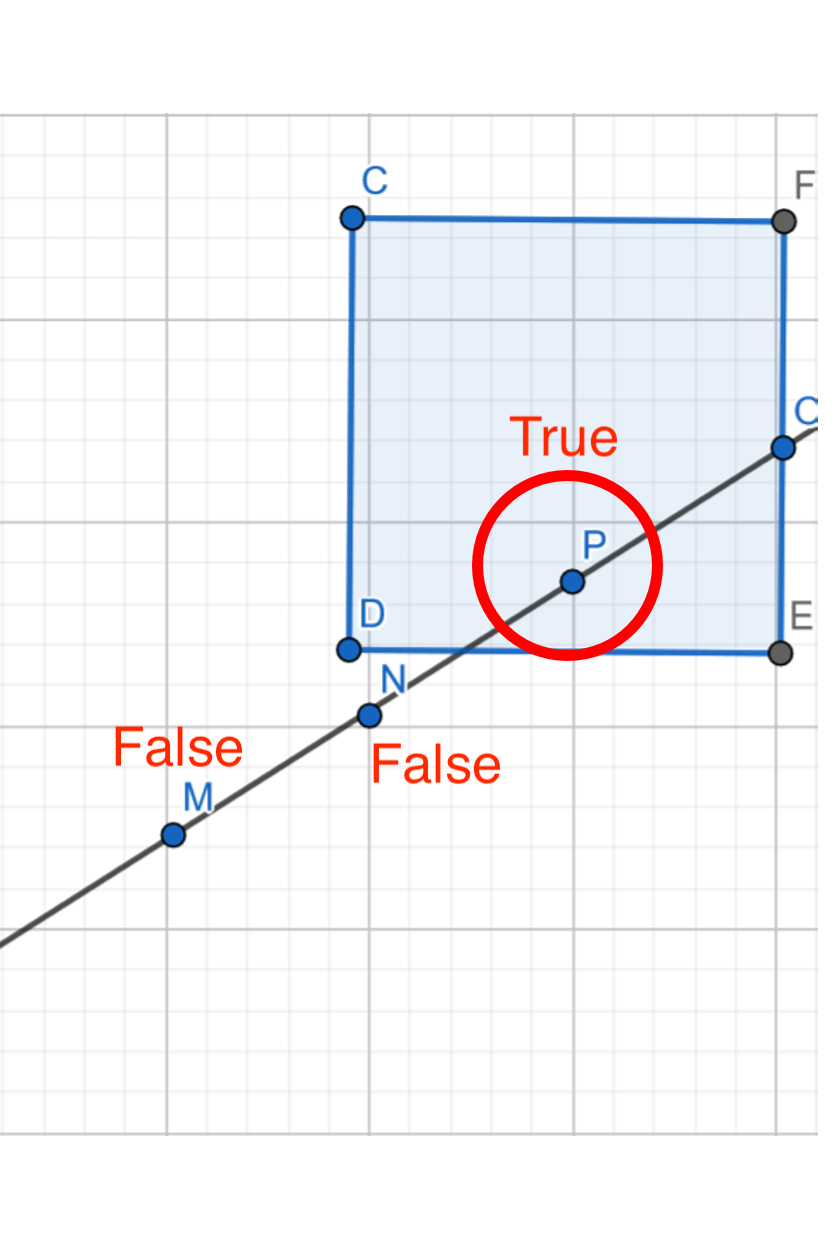
Solución:¶
def has_impact(x_ball, y_ball, x_pad, y_pad, pad_width, pad_height):
if x_ball >= x_pad and x_ball <= x_pad + pad_width:
if (y_pad - pad_height <= y_ball <= y_pad) or (y_pad <= y_ball <= y_pad + pad_height):
return True
return False
Podemos comprobar su funcionamiento pasando unas coordenadas y unas dimensiones que simulen ese impacto. Por ejemplo, tenemos una pelota que se encuentra en las coordneadas (10,2), mientras que nuestra raqueta tiene unas dimensiones de 4x2 y se encuentra en las coordenadas (8,0). Como hemos definido las coordenadas de la raqueta como el vértice inferior izquierdo, podemos calcular fácilmente cual es el rango de valores X e Y que ocupa su superficie. En este caso las X entre [8,8+4] y las Y entre [0, 0+2]. Como nuestra pelota está en las coordenadas (10,2) podemos concluir que sí que hay impacto:
has_impact(10, 2, 8, 0, 4, 2)
True
Sin embargo, si la pelota se encontara en la posición (14,2), se saldría por la derecha de la raqueta:
has_impact(14, 2, 8, 0, 4, 2)
False
O si se encontrara en la posición (7,2), se saldría por la izquierda de la raqueta:
has_impact(7, 2, 8, 0, 4, 2)
False
O si se encontrara en la posición (10,3), a nivel de las X sí que se encontaría alineada con la raqueta, pero a nivel de las Y todavía no habría entrado en contacto con ella
has_impact(10, 3, 8, 0, 4, 2)
False
Tip
Si lo piensas un poco, entenderás como la función has_impact también sirve para detectar el impacto de la pelota con los ladrillos. En lugar de pasarle las coordenadas y dimensiones de la raqueta le podemos pasar las coordenadas y las dimensiones de uno de los ladrillos y el funcionamiento será exactamente el mismo.
2.7. Siguiente posición de la pelota¶
En este apartado vamos a implementar la función calc_ball_position_with_angle() que calcula la posición de la pelota en el siguiente instante. Para ello, tenemos que tener en cuenta si se mueve hacia la pared de ladrillos o hacia la raqueta (game_params[“ball_sloping_positive”]), su ángulo (game_params[“ball_angle”]) y su velocidad (game_params[“ball_speed”]).
Como todas estas variables forman parte del diccionario game_params que estamos usando como variable global, no es necesario que le pasemos ningún argumento de entrada a la función. Por otro lado, la función debe devolver una tupla con la posición de la pelota en el instante siguiente.
Solución:¶
def calc_ball_position_with_angle():
x_delta = math.cos(math.radians(game_params["ball_angle"])) * game_params["ball_speed"]
y_delta = math.sin(math.radians(game_params["ball_angle"])) * game_params["ball_speed"]
if game_params["ball_sloping_positive"]:
y_delta = -y_delta
return x_delta, y_delta
2.8. Impacto con los ladrillos¶
La función que vamos implementar ahora es la encargada de gestionar el choque de la pelota con los ladrillos. La función handle_impact_target() tiene que comprobar si la pelota ha colisionado con alguno de los objetivos y si es así:
Eliminar ese objetivo de las listas de objetivos
Recalcular el ángulo de rebote de la pelota
Invertir el valor de la variable clave “ball_sloping_positive”
Note
Dependiendo del padding que estés usando entre tus objetivos, es posible que la pelota esté en contacto con dos o más objetivos. En ese caso puedes asumir que solo está impactando con uno de ellos.
Solución:¶
def handle_impact_target():
i=0
target_touched = False
while i < len(game_params["targets_on_map"]) and not target_touched:
target = game_params["targets_on_map"][i]
if has_impact(game_params["ball_position_x"], game_params["ball_position_y"], target[0], target[1], game_params["target_width"], game_params["target_height"]):
target_touched = True
game_params["targets_on_map"].pop(i)
game_params["ball_angle"] = calc_ball_rebound_angle()
game_params["ball_sloping_positive"] = not game_params["ball_sloping_positive"]
i+=1
Note
La variable target_touched la estamos usando para salir del bucle en cuanto hayamos detectado un ladrillo que ha impactado con la pelota. En caso de querer deshabilitar esta simplificación, podemos eliminar esta variable para que cada vez que la pelota entre en contacto con varios ladrillos, los elimine de golpe.
2.9. Impacto con la raqueta¶
De manera similar al apartado anterior, vamos a codificar la función handle_impact_pad() que se encarga de detectar si la pelota ha impactado con laraqueta y en ese caso:
Cambiar el ángulo de rebote de la pelota
Cambiar la dirección de la pelota
Solución:¶
def handle_impact_pad():
if has_impact(game_params["ball_position_x"], game_params["ball_position_y"],
game_params["pad_position_x"], game_params["pad_position_y"],
game_params["pad_width"], game_params["pad_height"]):
game_params["ball_angle"] = calc_ball_rebound_angle()
game_params["ball_sloping_positive"] = not game_params["ball_sloping_positive"]
2.10. Impacto con las paredes¶
El último elemento cuyos rebotes tenemos que gestionar son las paredes del recinto del juego. La función handle_impact_map_borders() se encarga de detectar si la pelota ha impactado con alguna de las paredes o el techo y en ese caso:
Si la pelota impacta con el borde superior, derecho o izquierdo:
Cambiar el angulo de la pelota
Cambiar el sentido de de la pelota
Si la pelota impacta con el borde inferior:
Cambiar el valor de “end_game” a True para indicar que la partida se ha acabado
Solución:¶
def handle_impact_map_borders():
if ((game_params["ball_position_x"] >= game_params["screen_width"]/2 - game_params["ball_radius"])
or (game_params["ball_position_x"] <= -game_params["screen_width"]/2 + game_params["ball_radius"])
or (game_params["ball_position_y"] >= game_params["screen_height"]/2 - game_params["ball_radius"])):
game_params["ball_angle"] = calc_ball_rebound_angle()
game_params["ball_sloping_positive"] = not game_params["ball_sloping_positive"]
elif game_params["ball_position_y"] <= -game_params["screen_height"]/2 + game_params["ball_radius"]:
game_params["end_game"] = True
2.11. Movimiento de la raqueta¶
Antes de implementar el juego completo, sólo nos queda programar el movimiento de la raqueta. Para ello vamos a implementar la función move_pad(delta) que permite modificar el valor de la clave “pad_position_x”. La función move_pad(delta) sólo recibe un argumento delta que indica la cantidad de desplazamiento que se debe aplicar a la posición del pad.
Tip
No se te olvide comprobar que tu raqueta no se desplaza más allá de los límites de la pantalla. Aunque en versiones modernas del juego esta era una de las funcionalidades extra que permitía pasar de pantalla sin necesidad de eliminar todos los ladrillos.
Solución:¶
def move_pad(delta):
if game_params["pad_position_x"] + delta >= -game_params["screen_width"]/2 - game_params["pad_width"]/2:
if game_params["pad_position_x"] + delta <= game_params["screen_width"]/2 - game_params["pad_width"]/2:
game_params["pad_position_x"] += delta
2.12. Reiniciar la partida¶
Vamos a codificar una última función new_game() que va a permitir reiniciar los ladrillos asi como volver a los valores por defecto de las variables game_params[“end_game”], game_params[“ball_position_x”] y game_params[“ball_position_y”]. Esta función la invocaremos cuando hayamos terminado una partida y queramos jugar de nuevo.
Solución:¶
def new_game():
if not (len(game_params["targets_on_map"]) > 0 and not game_params["end_game"]):
init_targets()
game_params["end_game"] = False
game_params["ball_position_x"] = 0
game_params["ball_position_y"] = 0
2.13. Crear el interfaz gráfico¶
Para la creación del interfáz gráfico y la construcción del juego, la librería tourtle te simplifica mucho la vida. Sólo tienes que definir una función drawAndPlay() que será la encargada de colocar los elementos visuales en la pantalla y definir la lógica del juego.
Podemos enumerar las tareas que tiene que realizar esta función:
Limpiar la pantalla
Si no quedan ladrillos en la pantalla, mostrar un mensaje para echar otra partida
Si quedan ladrillos en la pantalla, dibujar la pelota con la función draw_circle y los ladrillos y la raqueta con la función draw_rectangle
Invocar a las funciones handle_impact_target, handle_impact_pad y handle_impact_map_borders para calcular los impactos
Actualizar la posición de la pelota para el instante siguiente
Actualizar la posición de la raqueta
Nota que la función está programada implementando un único instante del juego. No hemos codificado ningún bucle, ya que esa funcionalidad queda oculta en el uso de la librería tourtle.
Solución¶
def drawAndPlay():
t.clear()
if len(game_params["targets_on_map"]) > 0 and not game_params["end_game"]:
#DRAWING
draw_circle(game_params["ball_position_x"], game_params["ball_position_y"], game_params['ball_radius'])
for target in game_params["targets_on_map"]:
draw_rectangle(target[0], target[1], game_params["target_width"], game_params["target_height"])
draw_rectangle(game_params["pad_position_x"], game_params["pad_position_y"], game_params["pad_width"], game_params["pad_height"])
# LOGIC
handle_impact_target()
handle_impact_pad()
handle_impact_map_borders()
x_delta, y_delta = calc_ball_position_with_angle()
game_params["ball_position_x"] += x_delta
game_params["ball_position_y"] += y_delta
else:
t.setpos(0, 0)
t.write("Play again? (press Y)", align="center", font=("Arial", 30, "bold"))
t.ontimer(drawAndPlay, 50)
t.done()
2.14. Juego completo¶
Como ya hemos adelantado, la librería tourtle simplifica mucho el diseño de videojuegos. No tenemos que implementar ningún bucle que simule el progreso del juego. Simplemente codificar la función drawAndPlay que posiciona los elementos y codifica la mecánica para un instante del juego.
Para poder disfrutar de nuesto programa sólo tenemos que definir las teclas de movimiento utilizando la función onkey de tourtle que permite asignar un comportamiento a la pulsación de una tecla. En nuestro caso:
Cada vez que pulsemos la tecla A se invocará a la función move_pad con un delta positivo (movimiento hacia la derecha)
Cada vez que pulsemos la tecla D se invocará a la función move_pad con un delta negativo (movimiento hacia la izquierda)
Cada vez que pulsemos la tecla Y se invocará a la función new_game que reinicia las variables del juego.
Tip
No está de más que te revises la documentación de tourtle porque hay funciones similares que realizan funciones diferentes. Por ejemplo:
t.onkey()
Sólo detecta una pulsación de cualquier tecla, mientras que la función:
t.onkeypress()
Detecta la pulsación individual y si la tecla se deja pulsada de manera permanente.
def main():
t.setup(game_params["screen_width"], game_params["screen_height"])
t.hideturtle()
t.tracer(False)
t.title("Arkanoid")
t.listen()
t.onkeypress(lambda: move_pad(game_params["pad_speed"]), "d")
t.onkeypress(lambda: move_pad(-game_params["pad_speed"]), "a")
t.onkey(new_game, "y")
drawAndPlay()
Para jugar sólo tienes que invocar a la función main().
main()
2.15. Extensiones del juego¶
El Arkanoid es un juego que se presta a multitud de mejoras. No hay más que ver las diferentes versiones que salieron al mercado y que todavía hoy se juegan en PCs y teléfonos móviles. Algunas de las modificaciones que puedes incluir son:
Diseñar un sistema de pantallas en el que vaya cambiando la distribución de los ladrillos
Modificar de manera aleatoria el ángulo de rebote para que no siempre sean los 175º que hemos utilizado. De esta manera aumentará la dificultad del juego
Puedes añadir nuevas teclas de movimiento que permita a la raqueta, por ejemplo, avanzar a saltos mayores, pausar el juego o añadir más pelotas para aumentar la dificultad
Las versiones modernas del Arkanoid descubrían unas píldoras con poderes especiales que caían al destruir algunos ladrillos. Estos poderes, en algunos casos eran positivos: que la pelota fuera más despacio, que la raqueta fuera más grande, permitir pasar automáticamente de pantalla… y en otros casos negativos: que la pelota fuera más rápida, que la raqueta fuera más pequeña o se moviera más despacio.
