Logo
Contents
2. Logo¶

Este capítulo va a ser una excepción porque no vamos a programar un juego, aunque el resultado va a ser tan entretenido como si lo fuera. Vamos a implementar una versión simplficada de un lenguaje de programacion!!. Y ese lenguage de programación va a ser el LOGO.
Es normal que no te suene. LOGO es un lenguaje de programación que fue diseñado en 1967 con fines educativos. Y fue muy conocido, principalmente, por sus capacidades gráficas.
Para dibujar programando en LOGO existían unas instrucciones que desplazaban por la pantalla una tortuga virtual que iba dejando un rastro que servía para componer dibujos. En nuestro caso, vamos a introducir estas instrucciones a través de una linea de comando. Estas instrucciones son:
Comando |
Descripción |
|---|---|
fd x |
forward => tortuga avanza x unidades |
bk x |
backward => tortuga retrocede x unidades |
rt x |
right => gira a la derecha x grados |
lt |
left => gira a la izquierda x grados |
Por ejemplo:
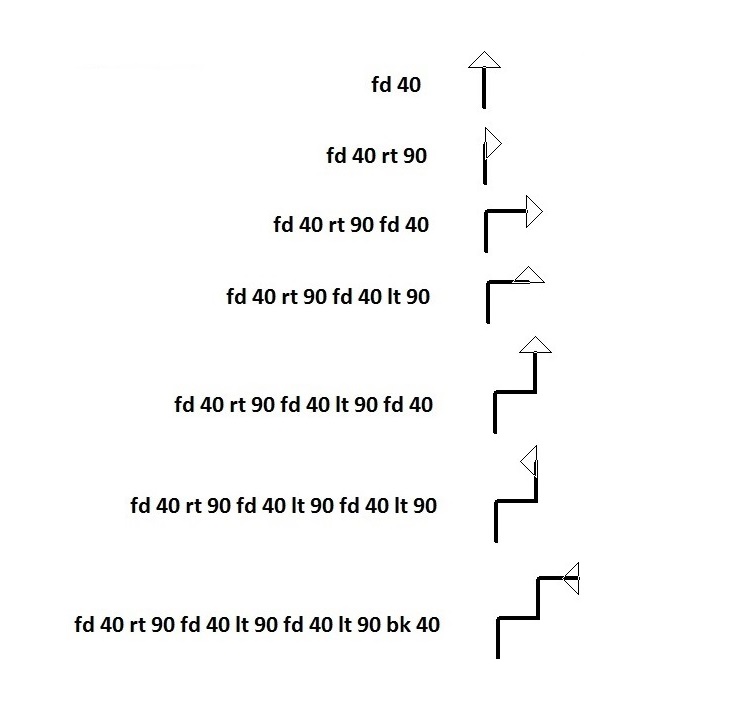
Combinando los comandos anteriores y utilizando diferentes desplazamientos y grados se pueden conseguir una gran variedad de diseños. También vamos a implementar una versión simplificada del comando repeat que sirve para repetir N veces una serie de movimientos proporcionados entre corchetes:
repeat N [ acc1 d1 acc2 d2 ]
Por ejemplo, el código:
repeat 4 [fd 100 rt 90]
Genera un cuadrado con una sóla instrucción:
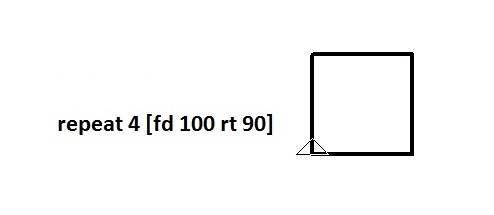
En el LOGO original existen muchas otras funciones que no vamos a programar como pero que puedes plantearte implementar para mejorar nuestra versión.
Comando |
Descripción |
|---|---|
pu |
penup (mover la tortuga sin dibujar) |
pd |
pendown (mover la tortuga dibujando) |
ht |
hideturtle (ocultar la tortuga) |
dt |
showturtle (mostrar la tortuga) |
See also
Puedes encontrar más información sobre este lenguanje de programación aquí
2.1. Dibujar trayectoria¶
Vamos a empezar escribiendo una función draw_coordinates(coordinates) que recibe como único argumento de entrada una lista de tuplas que contienen coordenadas (x,y). La función debe dibujar un grafico con matplotlib que conecte punto por punto cada tupla en el mismo orden en el que se proporcionan.
Por ejemplo:
draw_coordinates([(0,0),(1,1),(1,0),(2,1),(2,-1),(1,0),(1,-1),(0,0)])
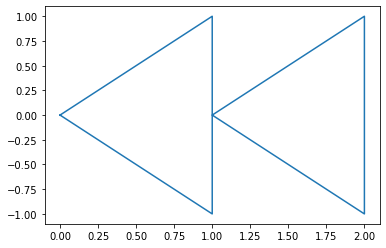
Puedes hacer el ejercicio de ir conectando las coordenadas del comando anterior y obtendrás la misma figura.
Solución:¶
import matplotlib.pyplot as plt
import math
def draw_coordinates(coordinates):
x, y = [],[]
for coor_x,coor_y in coordinates:
x.append(coor_x)
y.append(coor_y)
plt.plot(x,y)
plt.show()
2.2. Añade movimiento¶
El siguiente paso es construir la función move(distance, direction, coordinates, isForward). Esta función recibirá varios argumentos:
distance es una variable numérica que indica la distancia en la que debe moverse la tortuga
direction es una variable numérica contiene los grados en los que se realiza el movimiento. Para simplificar nuestra implementación vamos a suponer que la referencia en los grados es siempre la misma. Es decir, no es relativa a la visión de la tortuga, sino a la nuestra. Por lo que si queremos que la tortuga avance hacia la derecha, direction deberá ser cero, si queremos que suba direction será igual a 90, si queremos que avanze hacia la izquierda direction será igual a 180 y si queremos que baje, direction tomará el valor 270.
coordinates es una variable tipo LISST en la que se almacenan las coordenadas de los anteriores movimientos de la tortuga
isForward es una variable binaria que sólo puede tomar dos valores, 1 si queremos que la tortuga avance o -1 si queremos que retroceda
Con toda esta información, la función debe calcular las coordenadas del nuevo punto en el que se dentendrá la tortuga después de aplicar el movimiento descrito por las variables distance, direction y isForward respecto a la última posición conocida. Por lo que la salida de la función será la lista de coordenadas original más una coordenada nueva.
Por ejemplo. Vamos a dibujar un triángulo con vertices en las coordenadas [(1,1),(2,2),(3,1)]. Si lo pintamos obtenemos un triángulo sin base:
draw_coordinates([(1,1),(2,2),(3,1)])
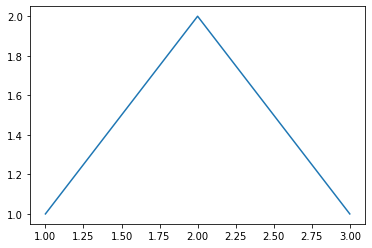
Tenemos que ejecutar una última instrucción para decirle a la tortuga de LOGO (que se encuentra en la coordenada (3,1)) que gire se desplace hacia la izquierda 2 unidades para que vuelva al punto de partida. Eso lo podemos hacer con el siguiente código:
coordinates=[(1,1),(2,2),(3,1)]
new_coordinates=move(2,180,coordinates, 1)
draw_coordinates(new_coordinates)
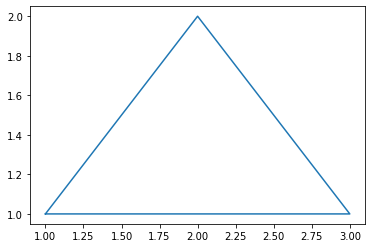
Si imprimimos la lista de nuevas coordenadas vemos que se ha añadido un nuevo punto que coincide con el punto de partida:
print(new_coordinates)
[(1, 1), (2, 2), (3, 1), (1.0, 1.0000000000000002)]
Tip
Recuerda que la dirección se la vamos a pasar en grados pero las funciones sin and cos utilizadas para calcular la nueva coordenada necesitan el ángulo en radianes.
Solución:¶
def move(distance, direction, coordinates, isForward):
new_coordinates = coordinates.copy()
direction = math.radians(direction)
x = math.cos(direction)*distance * isForward + new_coordinates[-1][0]
y = math.sin(direction)*distance * isForward + new_coordinates[-1][1]
new_coordinates.append((x,y))
return new_coordinates
2.3. Línea de comandos¶
Para que el usuario introduzca las instrucciones de LOGO, en algún momento del programa principal invocaremos una instrucción input. El usuario puede introducir una única instrucción o una lista de ellas. Para identificar las instrucciones, vamos a construir la función get_instructions(user_input). Esta función recibe como argumento una variable STRING con el comando o los comandos introducidos por el usuario. La función debe utilizar la función split para separar el comando de LOGO por espacios. La función get_instructions(user_input) devuelve una lista de enteros que se corresponden con las posiciones de los elementos de la variable user_input que se corresponden con comandos de LOGO.
Por ejemplo:
get_instructions("fd 40 rt 30 bk 12 lt 180 fd 57 repeat 4 [fd 100 rt 90]")
[0, 2, 4, 6, 8, 10]
Los valores devueltos por el comando anterior se corresponden con las posiciones de los comandos fd, rt, bk, lt, fd y repeat en la lista [‘fd’, ‘40’, ‘rt’, ‘30’, ‘bk’, ‘12’, ‘lt’, ‘180’, ‘fd’, ‘57’, ‘repeat’, ‘4’, ‘[fd’, ‘100’, ‘rt’, ‘90]’].
Tip
La manera mas sencilla es implementar un bucle después de hacer un split e ir chequeando cuales de los elementos separados son comandos y cuales no.
Note
Por simplificar, asumimos que si la secuencia de instrucciones contiene el comando repeat, este aparecerá siempre como la última instrucción o como única instrucción.
Solución:¶
def get_instructions(user_input):
index = []
current_index = 0
user_input_split = user_input.split(' ')
while current_index < len(user_input_split):
if user_input_split[current_index].lower() in ['fd', 'bk', 'rt', 'lt']:
index.append(current_index)
current_index +=2
elif user_input_split[current_index].lower() == 'repeat':
index.append(current_index)
break
return index
2.4. Decodificar el comando¶
La parte más complicada de un lenguaje de programación es implementar la forma en la que se intepretan los comandos. En nuestro caso tenemos que conseguir traducir los comandos que hemos introducido y convertirlos en llamadas a la función move.
Para ello vamos a implementar la función decode_input(user_input, coordinates, direction) que recibe los siguientes argumentos de entrada:
user_input contiene la variable string con las instrucciones introducidas por el usuario
coordinates con la lista de coordenadas realizadas por la tortuga
direction con la última orientación de la tortuga. Esta variable es especialmente importante en los comandos “fd” y “bk” en los que la tortuga debe seguir o retroceder en la misma dirección que llevaba en el último movimiento.
La función devolverá una tupla con dos elementos:
new_coordinates con una lista con las coordenadas actualizadas
new_orientation con la última orientación de la tortuga.
Esta función debe utilizar la función get_instructions para obtener las posiciones de los comandos de LOGO, interpretarlos y actualizar la posición y la orientación de la tortuga.
Vamos a intentar explicarlo mejor con un ejemplo. Vamos a intentar dibujar una escalera como esta:
draw_coordinates([(0, 0), (5, 0), (5, 5), (10, 5)])

El primer comando define el desplazamiento de 5 unidades en la dirección inicial (direction = 0)
decode_input("fd 5", [(0,0)], direction=0)
([(0, 0), (5.0, 0.0)], 0)
El segundo comando define un giro a la izquierda de 90 grados. Fijate como este comando no añade una coordenada nueva pero sí actualiza la orientación de la tortuga
decode_input("fd 5 lt 90", [(0,0)], direction=0)
([(0, 0), (5.0, 0.0)], 90.0)
El tercer comando define un avance en vertical de 5 unidades, sin afectar a la orientación de la tortuga que sigue valiendo 90 grados
decode_input("fd 5 lt 90 fd 5", [(0,0)], direction=0)
([(0, 0), (5.0, 0.0), (5.0, 5.0)], 90.0)
El cuarto comando gira la tortuga 90 grados hacia la derecha devolviendo la orientación de la tortuga a los 0 grados originales
decode_input("fd 5 lt 90 fd 5 rt 90", [(0,0)], direction=0)
([(0, 0), (5.0, 0.0), (5.0, 5.0)], 0.0)
Y el último comando avanza otras 5 unidades en la dirección original, terminando de construir la función escalón.
decode_input("fd 5 lt 90 fd 5 rt 90 fd 5", [(0,0)], direction=0)
([(0, 0), (5.0, 0.0), (5.0, 5.0), (10.0, 5.0)], 0.0)
Por último, vamos utilizar el comando repeat para construir una escalera de mayor tamaño, evitando tener que repetir varias veces los mismos comandos
new_coordinates, new_direction = decode_input("fd 5 lt 90 fd 5 rt 90 fd 5 repeat 2 [lt 90 fd 5 rt 90 fd 5]", [(0,0)], direction=0)
print(new_coordinates)
[(0, 0), (5.0, 0.0), (5.0, 5.0), (10.0, 5.0), (10.0, 10.0), (15.0, 10.0), (15.0, 15.0), (20.0, 15.0)]
draw_coordinates(new_coordinates)
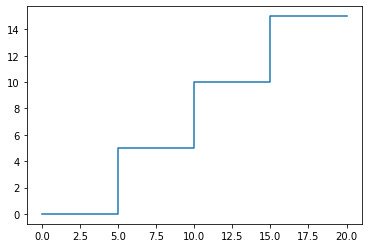
Como ves, el comando repeat es muy potente y nos va a proporcionar mucha capacidad de dibujo.
Solución:¶
def decode_input(user_input, coordinates, direction):
elements = user_input.split(' ')
new_coordinates = coordinates.copy()
instructions = get_instructions(user_input)
for i in instructions:
if elements[i].lower() == 'fd':
coordinates = move(float(elements[i+1]), direction, coordinates, 1)
elif elements[i].lower() == 'bk':
coordinates = move(float(elements[i+1]), direction, coordinates, -1)
elif elements[i].lower() == 'rt':
direction -= float(elements[i+1])
elif elements[i].lower() == 'lt':
direction += float(elements[i+1])
elif elements[i].lower() == 'repeat':
repetitions = int(elements[i+1])
command_to_repeat = " ".join(elements[i+2:])[1:-1]
for repetition in range(repetitions):
coordinates, direction = decode_input(command_to_repeat, coordinates, direction)
return coordinates, direction
2.5. Programa principal¶
Ya sólo nos queda construir el programa principal. La estructura es un bucle infinito en el que el usuario puede introducir comandos LOGO y la aplicación los interpreta. Para evitar que nuestro programa se quede bloqueado, tendrás que añadir la posibilidad de salir del blucle infinito cuando el usuario introduzca una x cen lugar de un comando de LOGO.
Solución:¶
print('Welcome to our LOGO interpreter:')
user_input = ''
movements = [(0,0)]
tourtle_orientation = 0
while True:
user_input = input('Input a LOGO command to move the tourtle (or x to exit): ')
if user_input != 'x':
movements, tourtle_orientation = decode_input(user_input, movements, tourtle_orientation)
draw_coordinates(movements)
else:
break
Welcome to our LOGO interpreter:
Input a LOGO command to move the tourtle (or x to exit): repeat 12 [rt 150 fd 100]
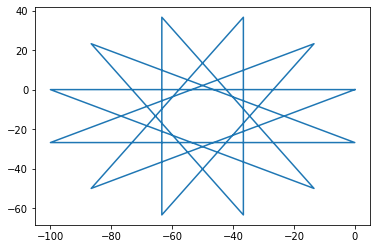
Input a LOGO command to move the tourtle (or x to exit): repeat 5 [fd 100 rt 72]
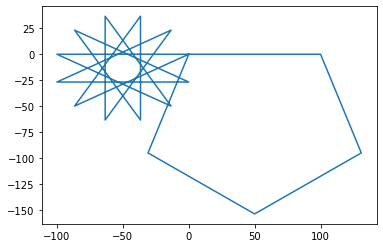
Input a LOGO command to move the tourtle (or x to exit): x
Note
Como la ejecución de los notebooks de Jupyter se realiza en celdas, si nuestro código invoca dos veces al comando plt.plot(), esto se va a traducir en una nueva figura, como en el ejemplo anterior.
Para resolverlo, vamos a utilizar el siguiente comando para eliminar el contenido de la celda antes de hacer el plt.plot() de la nueva. De esta forma, el usuario tendrá la impresión de que el entorno de dibujo es único.
from IPython.display import clear_output
clear_output(wait=True)
from IPython.display import clear_output
print('Welcome to our LOGO interpreter:')
user_input = ''
movements = [(0,0)]
tourtle_orientation = 0
while True:
user_input = input('Input a LOGO command to move the tourtle (or x to exit): ')
if user_input != 'x':
movements, tourtle_orientation = decode_input(user_input, movements, tourtle_orientation)
clear_output(wait=True)
draw_coordinates(movements)
else:
break
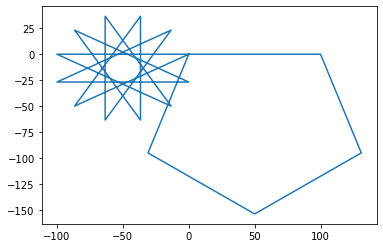
Input a LOGO command to move the tourtle (or x to exit): x
Si vuelves a introducir los mismos comandos que el primer ejemplo, verás que las figuras ya no se acumulan sino que desaparecen para que la nueva figura ocupe su lugar.
2.6. Extensiones del Juego¶
De todos los capítulos de este libro, este es el más sencillo de extender ya que los lenguajes de programación se pueden complicar tanto como queramos. Podemos añadir más comandos a nuestro interprete de logo, algunos reales del LOGO original y otros inventados definidos por nosotros mismos. Otra posibilidad es añadir funcionalidades nuevas a nuestro programa principal. Aquí te damos algunas ideas:
Mejora la función decode_input para poder introducir comandos de tipo repeat en cualquier posición
Busca alguna referencia del LOGO original e intenta implementar más comandos
Puedes añadir comandos inventados, por ejemplo “poly N”. Este comando dibujará un polinomio del número de lados indicado
Puedes añadir comandos para del diseño de fractales. Este comando sería muy similar al comando repeat, pero modificando las dimensiones de los movimientos.
Puedes añadir más funcionalidades al programa principal, por ejemplo: borrar la pantalla, seleccionar el color de la línea que va dejando la tortuga, salvar el dibujo realizado como un fichero JPG,…
